（三）数据结构之队列

发表于 | 更新于 | 分类于 | 阅读次数：
本文字数： 1.1k | 阅读时长 ≈ 2 分钟
  此文待重构

简介

  队列，又称为伫列（queue），是先进先出（FIFO, First-In-First-Out）的线性表。在具体应用中通常用链表或者数组来实现。队列只允许在后端（称为rear）进行插入操作，在前端（称为front）进行删除操作。

特点

  • 队列是一种线性结构
  • 相比数组，队列中允许的操作为数组的操作子集
  • 只能从一端（队尾）添加元素，只能从另一端（队首）取出元素
  • 队列是一种先进先出（FIFO，First In First Out）的数据结构

操作

  队列数据结构使用两种基本操作：：

  • 进队（enqueue）：将数据从队尾插入，队列元素加 1
  • 出队（dequeue）：将数据从队首移出，队列元素减 1

图示

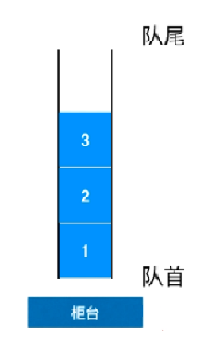
  队列类似日常排队一样，人们遵守规则，后来的人排最后，不能插队，队首的人事情办好则出队。

类别

  • 顺序队列：在顺序队列中，出队操作后又进行入队操作，当队尾指针已经到数组的上界，不能再有入队操作，但其实数组中还有空位置，存在“假溢出”现象（如下图），解决假溢出的途径—-采用循环队列
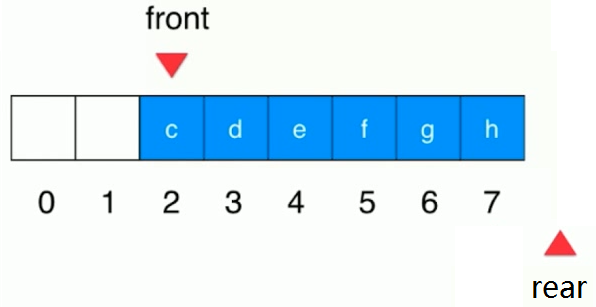
  • 循环队列：
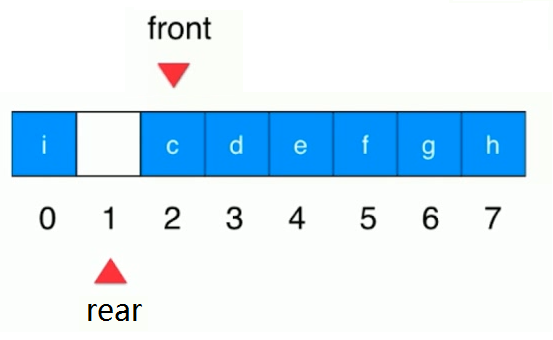
  • 臆想成环：

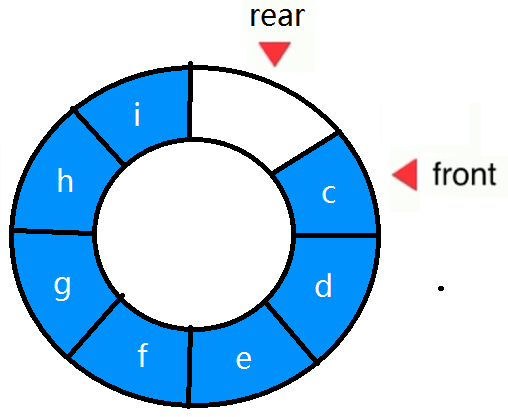
  在循环队列中，空队特征是front = rear, 队满时也会有front = rear，判断条件将出现二义性。
  解决方案有三种：

  1. 加设标志位，让删除动作使其为1，插入动作使其为0， 则可识别当前front == rear;
  2. 使用一个计数器记录队列中元素个数（即队列长度）
  3. 人为浪费一个单元，令队满特征为 front = (rear +1)%length(数组长度)—空闲单元法
    这里采用空闲单元法解决二义性问题。

代码实现（循环队列）

  接口定义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
public interface Queue<E> {
    int size();
    boolean isEmpty();
    void enqueue(E e);
    E dequeue();
    E getFront();
}
public class LoopQueue<E> implements Queue<E>{
    private E[] queue;
    private int front, rear;//队首，队尾指针
    private int size;//元素个数

    /**
     * 队列容量为capaCity
     *因为要人为浪费一个单元，所以new的
     *时候+1
     * @param capacity
     */
    public LoopQueue(int capacity) {
        queue = (E[]) new Object[capacity + 1];
    }

    //队列容量无参时初始为10
    public LoopQueue() {
        this(10);
    }

    //队列是否为空
    public boolean isEmpty() {
        return front == rear;
    }

    //队列元素个数
    public int size() {
        return size;
    }

    //队列容量
    public int getCapacity() {
        return queue.length - 1;
    }

    //元素入队尾
    public void enqueue(E e) {
        if ((rear + 1) % queue.length == front) {
            throw new IllegalArgumentException("Queue is full,enqueue is failed");
        }
        queue[rear] = e;
        rear = (rear + 1) % queue.length;
        size++;
    }

    //元素出队首
    public E dequeue() {
        if (isEmpty()) {
            throw new IllegalArgumentException("Queue is empty,dequeue is failed");
        }
        E ret = queue[front];
        queue[front] = null;
        front = (front + 1) % queue.length;
        size--;
        return ret;
    }

    //查看队首元素
    public E getFront() {
        return queue[front];
    }

    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append(String.format("Queue size = %d,capacity = %d\n", size, getCapacity()));
        res.append("front [");
        for (int i = front; i != rear; i = (i + 1) % queue.length) {
            res.append(queue[i]);
            if ((i + 1) % queue.length != rear) {
                res.append(',');
            }
        }
        res.append("] rear");
        return res.toString();
    }
}

为了使该队列能动态增减，加入以下优化:

1
2
3
4
5
6
7
8
9
10
11
//队列扩容
    public void resize(int newCapacity) {
        E[] newQueue = (E[]) new Object[newCapacity + 1];
        //将旧队列队首(可能不再数组首位置)元素放入新队列第一个位置
        for (int i = 0; i < size; i++) {
            newQueue[i] = queue[(i + front) % queue.length];
        }
        queue = newQueue;
        front = 0;
        rear = size;
    }

enqueue优化：

1
2
3
4
5
6
7
8
9
//元素入队尾
   public void enqueue(E e) {
       if ((rear + 1) % queue.length == front) {
           resize(2 * getCapacity());
       }
       queue[rear] = e;
       rear = (rear + 1) % queue.length;
       size++;
   }

dequeue优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//元素出队首
    public E dequeue() {
        if (isEmpty()) {
            throw new IllegalArgumentException("Queue is empty,dequeue is failed");
        }
        E ret = queue[front];
        queue[front] = null;
        front = (front + 1) % queue.length;
        size--;
        if (size == getCapacity() / 4 && getCapacity() / 2 != 0) {
            resize(getCapacity() / 2);
        }
        return ret;
    }

测试代码

1
2
3
4
5
6
7
8
9
10
11
12
@Test
public void test() {
    LoopQueue<Integer> queue = new LoopQueue<>();
    for (int i = 0; i < 10; i++) {
        queue.enqueue(i);
        System.out.println(queue);
        if (i % 3 == 2) {
            queue.dequeue();
            System.out.println(queue);
        }
    }
}

测试结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Queue size = 1,capacity = 10
front [0] rear
Queue size = 2,capacity = 10
front [0,1] rear
Queue size = 3,capacity = 10
front [0,1,2] rear
Queue size = 2,capacity = 5
front [1,2] rear
Queue size = 3,capacity = 5
front [1,2,3] rear
Queue size = 4,capacity = 5
front [1,2,3,4] rear
Queue size = 5,capacity = 5
front [1,2,3,4,5] rear
Queue size = 4,capacity = 5
front [2,3,4,5] rear
Queue size = 5,capacity = 5
front [2,3,4,5,6] rear
Queue size = 6,capacity = 10
front [2,3,4,5,6,7] rear
Queue size = 7,capacity = 10
front [2,3,4,5,6,7,8] rear
Queue size = 6,capacity = 10
front [3,4,5,6,7,8] rear
Queue size = 7,capacity = 10
front [3,4,5,6,7,8,9] rear

时间复杂度分析

操作 时间复杂度
void enqueue(E) O(1) 均摊
E dequeue() O(1) 均摊
E getFront() O(1)
int getSize() O(1)
boolean isEmpty() O(1)

基于堆的优先队列

请了解堆后再看后续代码，在后续章节有说明(八)数据结构之堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {
    private MaxHeap<E> maxHeap;

    public PriorityQueue() {
        maxHeap = new MaxHeap<>();
    }

    @Override
    public int size() {
        return maxHeap.size();
    }

    @Override
    public boolean isEmpty() {
        return maxHeap.isEmpty();
    }
    
    @Override
    public void enqueue(E e) {
        maxHeap.add(e);
    }

    @Override
    public E dequeue() {
        return maxHeap.extractMax();
    }

    @Override
    public E getFront() {
        return maxHeap.findMax();
    }
}

文章信息

时间 说明
2018-12-02 初稿
0%