（五）数据结构之二叉搜索树

发表于 | 更新于 | 分类于 | 阅读次数：
本文字数： 2.2k | 阅读时长 ≈ 3 分钟

简介

  在计算机科学中，二叉树（英语：Binary tree）是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序，不能随意颠倒。

特点

  • 天然递归结构
  • 动态数据结构
  • 具有唯一根节点
  • 每个节点最多有 2 个孩子
  • 每个节点最多有一个父亲
  • 每个节点的左子树或右子树也是二叉树
  • 二叉树不一定是“满”的

图示

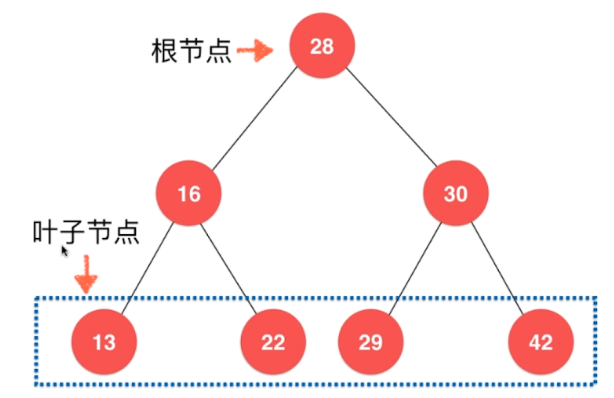
二叉搜索树特点

  • 二叉搜索树是二叉树的一种

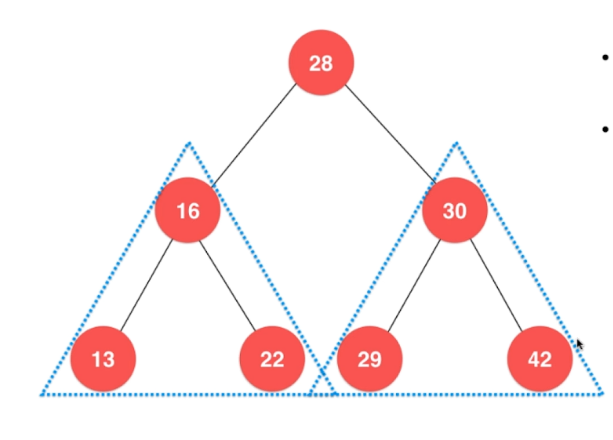
  • 每一颗子树也是二叉搜索树

  • 存储的元素必须有可比较性

  • 二叉搜索树的每个节点的值：大于其左子树的所有节点的值，小于其右子树的所有节点的值，如下图：

设计思路

实现步骤

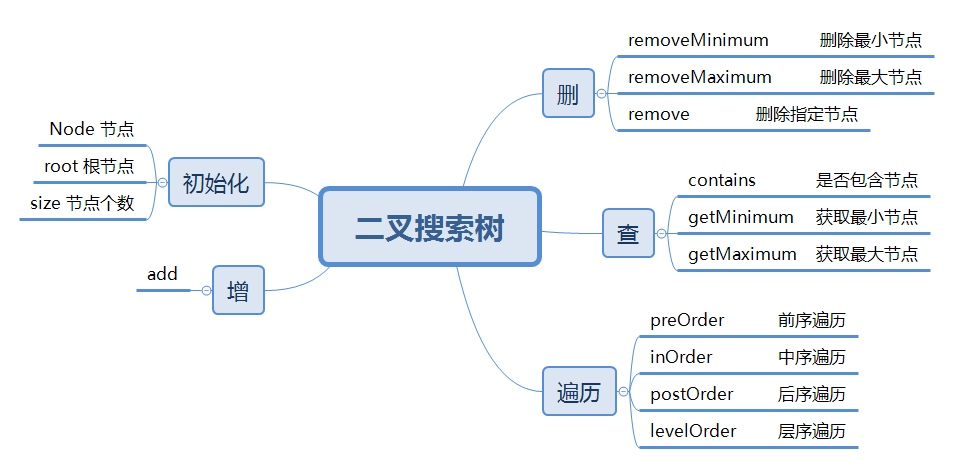
  设计思路基本遵循上面思维导图的描述，但在具体实现过程中，我们需要额外考虑一些问题：

  • 树的底层使用什么数据结构更合适？
    • 数组？
    • 链表？
  • 如何将数据存储到树中？
    • 应该以什么方式进行数据存储？
      • 递归？
      • 非递归？
  • 如何查询获取到树中的数据？
    • 查询什么样的数据？
      • 最小值？
      • 最大值？
      • 指定值？
    • 如果查询的数据不存在，应该返回什么样的结果？
    • 需要查询显示什么样的结果？为什么需要这种结果？
    • 使用什么样的顺序去查询数据？是依次一查到底？还是一级一级查？
  • 如何删除树中的数据？
    • 删除什么样的数据？
      • 最大值？
      • 最小值？
      • 指定值？
    • 删除数据后会不会导致到树结构的松动，需不需要一些额外措施处理？

  上面的问题一步一步理清后，我们就可以进行代码实现了。

代码实现

基本定义

  二叉树和链表一样，同样可由节点组成，只是树的节点存在根节点，并且存在两个分别指向左右两个孩子的指针。

  下面，我们看下代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public class BinarySearchTree<E extends Comparable<E>> {
    // 定义节点
    private class Node {
        private E e;
        // 左右节点
        private Node left, right;

        public Node(E e) {
            this.e = e;
        }
    }
    
    // 根节点
    private Node root;
    // 节点的个数
    private int size;

    public BinarySearchTree() {

    }

    // 获取节点的个数
    public int size() {
        return size;
    }

    // 判空
    public boolean isEmpty() {
        return size == 0;
    }

}

增加节点

  

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 增加一个值为 e 的节点
public void add(E e) {
    root = add(root, e);
}

private Node add(Node node, E e) {
    if (node == null) {
        size++;
        return new Node(e);
    } else if (e.compareTo(node.e) < 0) {
        node.left = add(node.left, e);
    } else if (e.compareTo(node.e) > 0) {
        node.right = add(node.right, e);
    }
    return node;
}

// 是否包含值为 e 的节点
public boolean contains(E e) {
    return contains(root, e);
}

private boolean contains(Node node, E e) {
    if (node == null) {
        return false;
    }
    if (e.compareTo(node.e) == 0) {
        return true;
    } else if (e.compareTo(node.e) < 0) {
        return contains(node.left, e);
    } else {
        return contains(node.right, e);
    }
}

删除节点

  要想删除一个节点，我们先聊一聊怎么获取最小最大节点。由二叉搜索树的定义知道：二叉搜索树的每个节点的值大于其左子树的所有节点的值，小于其右子树的所有节点的值，那么最小的值一定在最左下角的那个节点里，最大的值一定在最右下角的那个节点里，所以有以下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 获取最小节点
public E getMinimum() {
    if (size == 0) {
        throw new IllegalArgumentException("BST is empty!!!");
    }
    return getMinimum(root).e;
}

private Node getMinimum(Node node) {
    if (node.left == null) {
        return node;
    } else {
        return getMinimum(node.left);
    }
}

// 获取最大节点
public E getMaximum() {
    if (size == 0) {
        throw new IllegalArgumentException("BST is empty!!!");
    }
    return getMaximum(root).e;
}

private Node getMaximum(Node node) {
    if (node.right == null) {
        return node;
    } else {
        return getMaximum(node.right);
    }
}

  那我们怎么删除一个值最小的节点或一颗最大的节点呢？
分2种情况：

  • 如果该最小(大)节点没有孩子，直接删除，下图最小节点13，最大节点42

img

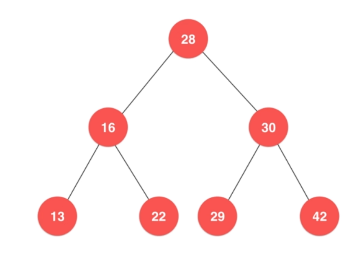
  • 如果该最小(大)节点有右(左)孩子，将右(左)孩子上移到它的位置

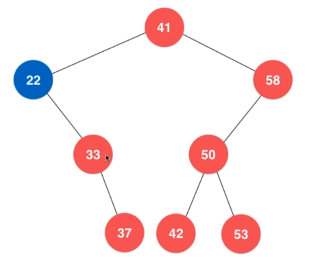
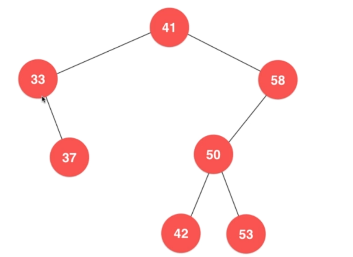
  转换成代码逻辑：如果当前节点的的左子树为 null，代表该节点为最小节点，返回该节点的右子树(右子树为null返回的也是null,相当于直接删除该节点),不为null代表该节点不是最小节点，递归当前节点的左节点，最后返回当前节点(递归到底层再回溯)

  上述为删除最小节点，删除最大节点与其原理相反。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// 返回删除的最小节点值
public E removeMinimum() {
    E ret = getMinimum();
    removeMinimum(root);
    return ret;
}

// 删除二叉树中最小节点
private Node removeMinimum(Node node) {
    if (node.left == null) {
        Node rightNode = node.right;
        node.right = null;
        size--;
        return rightNode;
    }
    node.left = removeMinimum(node.left);
    return node;
}

// 返回删除的最大节点值
public E removeMaximum() {
    E ret = getMaximum();
    removeMaximum(root);
    return ret;
}

// 删除二叉树中最大节点
private Node removeMaximum(Node node) {
    if (node.right == null) {
        Node leftNode = node.left;
        node.left = null;
        size--;
        return leftNode;
    }
    node.right = removeMaximum(node.right);
    return node;
}

  好了，现在我们可以开始删除想删的节点了！分为3种情况：

  • 删除只有左孩子的节点
  • 删除只有右孩子的节点
  • 删除具有左孩子和右孩子的节点，如下图：

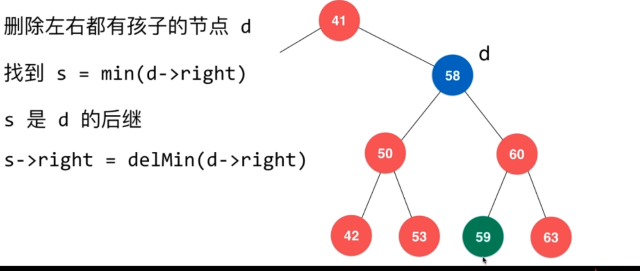
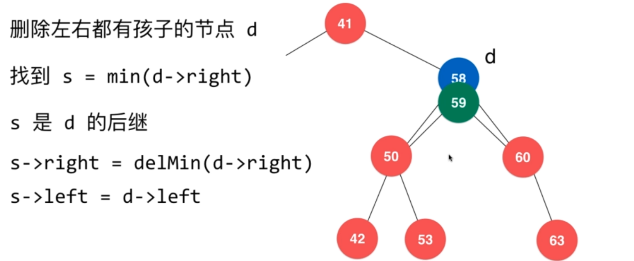
  前两种均以在前面讨论过，这里只讨论第 3 种情况：
  如果该节点既有左孩子又有右孩子，找到右孩子中值最小的节点，用它顶替该节点(当然也可以找到左孩子中值最大的节点，用它顶替该节点，2种方法2选1)由于前面我们写了怎么找树中最小节点或最小节点的方法，这里就可以拿来用啦

  删除代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// 删除包含指定值的节点
public void remove(E e) {
    root = remove(root, e);
}

private Node remove(Node node, E e) {
    if (node == null) {
        return null;
    }
    if (e.compareTo(node.e) < 0) {
        node.left = remove(node.left, e);
        return node;
    } else if (e.compareTo(node.e) > 0) {
        node.right = remove(node.right, e);
        return node;
    } else {//e.compareTo(node.e) == 0
        if (node.left == null) {
            Node rightNode = node.right;
            node.right = null;
            size--;
            return rightNode;
        }
        if (node.right == null) {
            Node leftNode = node.left;
            node.left = null;
            size--;
            return leftNode;
        }
        // 代替的节点为 node 节点的右子树中最小节点
        Node successsor = getMinimum(node.right);
        // 将 node 节点的右子树中的最小节点删除
        // 同时将删完最小节点的右子树赋予代替节点的右子树
        successsor.right = removeMinimum(node.right);
        // 代替节点的左子树为node节点的左子树
        successsor.left = node.left;
        // 断开node节点同二叉树的联系
        node.left = node.right = null;

        return successsor;
    }
}

二叉树遍历

  二叉树的遍历分为：

  • 前序遍历（DLR）
  • 中序遍历（LDR）
  • 后序遍历（LRD）
  • 层序遍历

前序遍历（DLR）

  定义：二叉树遍历的一种，也叫做先根遍历、先序遍历、前序周游，可记做根左右。
  步骤：前序遍历首先访问根结点，之后遍历左子树，最后遍历右子树。

  代码实现（基于源代码）：

1
2
3
4
5
6
7
8
9
10
11
12
13
//前序遍历
public void preOrder(){
        preOrder(root);
}

private void preOrder(Node node){
    if (node == null){
        return;
    }
    System.out.println(node.e);
    preOrder(node.left);
    preOrder(node.right);
}

中序遍历（LDR）

  定义：二叉树遍历的一种，也叫做中根遍历、中序周游。
  步骤：中序遍历首先遍历左子树，之后访问根结点，最后遍历右子树。

  代码实现（基于源代码）：

1
2
3
4
5
6
7
8
9
10
11
12
13
//中序遍历
public void inOrder(){
    inOrder(root);
}

private void inOrder(Node node) {
    if (node == null){
        return;
    }
    inOrder(node.left);
    System.out.println(node.e);
    inOrder(node.right);
}

后序遍历（LRD）

  定义：二叉树遍历的一种，也叫做后根遍历、后序周游，可记做左右根。
  步骤：先左后右再根，即首先遍历左子树，之后遍历右子树，最后访问根结点。

  后序遍历有递归算法和非递归算法两种，代码实现（基于源代码）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 后序遍历
public void postOrder(){
    postOrder(root);
}

// 递归实现
private void postOrder(Node node) {
    if (node == null){
        return;
    }
    postOrder(node.left);
    postOrder(node.right);
    System.out.println(node.e);
}

层序遍历

  定义：也叫广度优先遍历。
  设二叉树的根节点所在层数为 1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第 2 层的节点，接着是第三层的节点，以此类推。自上而下，自左至右逐层访问树结点的过程就是层序遍历。

  代码实现（基于源代码）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//层序遍历
public void levelOrder(){
    Queue<Node> queue = new LinkedList<>();
    queue.add(root);
    while(!queue.isEmpty()){
        Node cur = queue.remove();
        System.out.println(cur.e);

        if(cur.left != null){
            queue.add(cur.left);
        }
        if(cur.right != null){
            queue.add(cur.right);
        }
    }
}

测试代码

1
2
3
4
5
6
7
8
9
10
@Test
public void test() {
    BinarySearchTree<Integer> bst = new BinarySearchTree<>();
    int[] array = {41, 22, 58, 15, 33, 50, 60, 13, 37, 42, 53, 59, 63};
    for (int a : array) {
        bst.add(a);
    }
    bst.remove(58);
    bst.levelOrder();
}

测试结果

1
2
3
4
5
6
7
8
9
10
11
12
41
22
59
15
33
50
60
13
37
42
53
63

  与预期相符。

文章信息

时间 说明
2018-12-07 初稿
0%